
第一章:引言
TextBook: Options, Futures and other derivatives 10th. Pearson
Derivatives are contracts which depend on varies values of underlying assets.
- CCPs: central counterparties
$$A<-> CCPs <-> B$$
- SEFs: swap executive facilities
1.1 types of traders in financial market and their function
- hedgers: hedging strategies using forward/future contracts, option
- speculators: same
- arbitrageurs: same traders introduce information into market while trading and help the market evolve to effective market.
第二章:期货市场和利用期货合约套期保值
2.1 外汇市场攻击路线
2.1.1 即期外汇市场攻击路线
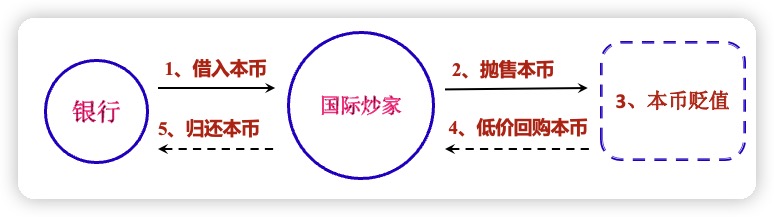
2.1.2 远期外汇市场和外汇期货市场的攻击路线
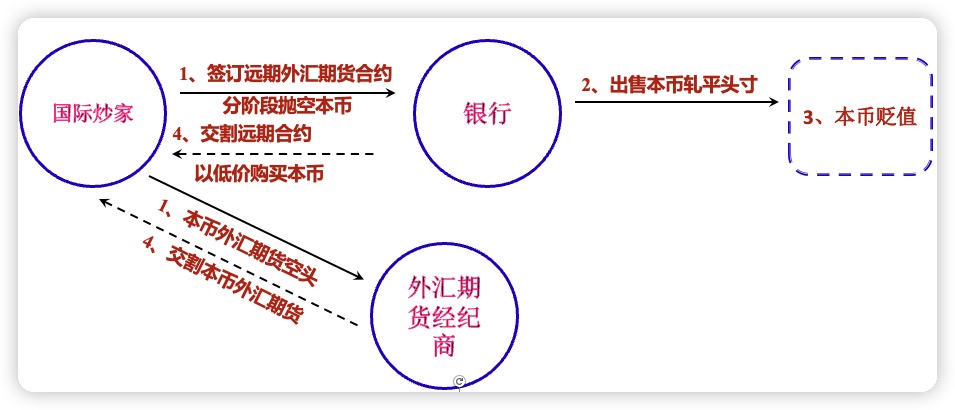
2.1.3 汇市和股市发动联合攻击的路线

2.2 期货交易流程

2.3 The Specification of the Futures Contract
- Key Concept
- Daily price Movement Limits
- Limit down(跌停板)
- Limit up(涨停板)
- A limit move(涨停板变动)
- The purpose of daily price limits is to prevent large price movements from occurring because of speculative excesses.
- Position Limits
- The purpose of the limits is to prevent speculators from exercising undue(不适当的) influence on the market.
- Daily price Movement Limits
2.4 Margin
Terminology
- Margin account(保证金帐户)
- Initial margin(初始保证金)
- Marking to market(盯市)
- Maintenance margin(维持保证金)
- Margin call(保证金催付)
- Variation margin(变动保证金) 规律:
- 持仓越多,保证金比率越高
- 距离交割日越近,保证金比率越高
2.4.1 The Operation of Margins
- Price(价格)
- Settlement price(结算价格)
- Lifetime highs and lows(有效期内的最高价和最低价)
- Open interest and volume of trading(未平仓合约数和交易量)
- Patterns of futures prices(期货价格模式)
Some terminology
- Opening price(开盘价)
- Settlement price(结算价格)
- the price just before the final bell each day used for the daily settlement process
- Open interest(未平仓合约数)
- the total number of contracts outstanding
- equal to number of long positions or number of short positions
- Normal market(正常市场)
- Inverted market(逆转市场)
2.4.2 Convergence Of Futures Price to Spot Price
As the delivery month of a futures contract is approached, the futures price (期货价格)converges to the spot price (现货价格)of the underlying asset. When the delivery period is reached, the futures price equals – or is very close to – the spot price.

2.5 Basis Risk
$$b = S - F$$
where:
- b : Basis 基差
- S: spot price of asset to be hedged
- F: Futures price of contract used
Some notation:
- F1 : Futures Price at time t1
- F2 : Futures Price at time t2
- S1 : Spot Price at time t1
- S2 : Spot price at time t2
- b1 : Basis at time t1
- b2 : Basis at time t2
We ignore the time value of money(货币时间价值)
2.5.1 A Short Position Hedger

The asset that gives rise to the hedger’s exposure is sometimes different from the asset underlying the hedge. The basis risk is then usually greater.
$$The\ effective\ price = S2 + F1 – F2$$
$$The\ effective\ price = F1 + (S2* – F2 ) + (S2 – S2* )$$
- S2* : The price of the asset underlying the futures contract at time $t_2$.
- S2 : The price of the asset being hedged at time $t_2$.
2.5.2 Minimum Variance Hedge Ratio
if an investor is to sell one unit of the asset, she has to short h units of the futures. The portfolio position at time $t_0$ is worth
$$\pi(t_0) = S(t_0) - hF(t_0,T)$$
where position at time $t_1$ will be worth 
The change in the value of the position will therefore be, and a short position will be

In both cases the variance of $\Delta \pi$ is equal to

Proportion of the exposure that should optimally be hedged is
$$h = \rho \frac{\sigma_S}{\sigma_F}$$
Optimal Number of Contracts 
Question

2.6 The Capital Market Line(CML)

2.7 Hedging an Equity Portfolio
Stock index futures can be used to hedge a well-diversified equity portfolio. Define:
- $V_A$: Current value of the portfolio
- $V_F$ : Current value of one futures contract (the futures price times the contract size)

Example



第三章:远期和期货价格 Forward and Futures Price
3.1 Consumption vs Investment Assets
- Investment assets are held by significant numbers of people purely for investment purposes (Examples: Stocks, Bonds, gold, silver)
- Consumption assets are held primarily for consumption (Examples: copper, oil)
3.2 Financial futures price
3.2.1 Measuring Interest Rates

3.2.2 Continuous Compounding

3.3 Some Inference
$$\beta_{im} = \frac{\sigma_{im}}{\sigma_{m}^2} = \rho \frac{\sigma_i \sigma_m}{\sigma_{m}^2} =\rho \frac{ \sigma_i}{\sigma_m} = h^*$$
$$N^* = \beta_{im}\frac{V_A}{V_F} = \frac{h^* V_A}{V_F}$$
$$R = \frac{P_{t+1}-P_t + D}{P_t}$$
$$E(ri) = r_f + \beta_{im}(E(r_m) -r_f)$$
3.4 The Arbitrage Formula
3.4.1 For financial futures
$$ F_0 = S_0 e^{rT}$$
$$ F_0 = S_0 e^{(r-q)T}$$
where q is the average yield during the life of the contract (expressed with continuous compounding)
Bond
$$ F_0 = (S_0-I) e^{rT}$$
Stock Index
$$ F_0 = S_0 e^{rT}\ where\ the\ S_0 \ is\ Stock\ Index$$
Forwards and Futures on Currencies
$$ F_0 = S_0 e^{(r-r_f)T}$$
3.4.2 For physical futures
Futures on Commodities
$$ F_0 = (S_0 + u) e^{rT}$$
or
$$ F_0 = S_0 e^{(r+u)T}$$
where u is storage cost
Convenience Yield
$$ F_0 = S_0 e^{(r+u - y)T}$$
Carry on Cost(interest rate+storage cost)
$$ F_0 = S_0 e^{(c-y)T}$$
第四章:期权价格特征 Option Price Characteristics
Question: Is $F_0 =^? E(S_T)$
| $F_0e^{-rT}$ | + long | |
|---|---|---|
| T | $F_0$ | $S_T$ |
| 0 | $F_0e^{-rT}$ | $S_Te^{-kT}$ |
$k = r_f + \beta(r_m - r_f)$
k is investor’s expected return
4.1 Option
4.1.1 The situations of option
- Out of money 虚值(若立即执行会亏损)
- In the money 实值
- At the money 两平
4.2 The value of option
Instrisic Value
call option :
$$max(S-X,0)$$
$$max(S - Xe^{-rT}, 0)$$
put option:
$$max(X-S,0)$$
$$max(Xe^{-rT} - S, 0)$$Time Value

4.2.1 Effect of Variables on Option Pricing

第五章:期权交易策略
5.1 Upper and Lower Bounds for Option Prices
Assumption:
- There are no transactions costs
- All trading profits(net of trading losses) are subject to the same tax rate
- Borrowing and lending are possible at the risk-free interest rate
5.1.1 Upper Bounds for Call Option
For call option, at any case, the option can never be worth more than the stock
$$c ≤ S0 \ and\ C ≤ S0$$
For put option
$P ≤ X$ for American option
$p ≤ Xe^{-rT}$ for European option
5.1.2 Lower Bounds for Call Option
A lower bound (下界)for the price of a European call option on a non-dividend-paying stock:
$$ c \geq max(S_0 - Xe^{-rt},0)$$
- Portfolio A: one call option with strike price X and an amount of cash equal to $Xe^{-rt}$
- Portfolio B: one share

5.2 Put-Call Parity
$$ C + Xe^{-rT} = P + S$$
第六章:二叉树模型介绍
6.1 Binomial Trees Pricing Model
6.1.1 Risk-Neutral Valuation

6.1.2 Self-Financing

第七章:股价行为模型 Model of behavior of stock price
7.1 Markov Property and Wiener Process

A Markov process (马尔可夫过程)is a particular type of stochastic process where only the present value of a variable is relevant for predicting the future
7.1.1 Weak-Form Market Efficiency
Weak-Form Market Efficiency(弱市场有效) means that the set of information only contains history of price and revenue ; that is, the present price reflects the information about all the history record of securities.
7.1.2 A Wiener Process

7.1.2.1 Properties of a Wiener Process

$$dz = \epsilon \sqrt{dt}$$
$E[(dz)] = 0$ and $var[(dz)] = dt$
7.2 Process for Stock Price
7.2.1 Ito Process

7.2.2 An Ito Process for Stock Prices

7.3 Ito’s Lemma
If we know the stochastic process followed by x, Ito’s lemma tells us the stochastic process followed by some function G (x, t )
Since a derivative security is a function of the price of the underlying asset and time, Ito’s lemma plays an important role in the analysis of derivative securities
1 A Taylor’s series expansion of G(x, t) gives
2 Substituting for $\Delta x$

3 The $\epsilon^2 \Delta t$ Term

4 Taking Limits
第八章:Black-Scholes公式 Black-Scholes formula
8.1 Lognormal Property
8.1.1 The Stock Price Assumption
$$\Delta S = \mu S\Delta t + \sigma S \epsilon \sqrt{\Delta t}$$
In a short period of time of length $\Delta t$, the return on the stock is normally distributed:
$$\frac{\Delta S}{S} /~ \phi(\mu \Delta t, \sigma \sqrt{\Delta t})$$
8.1.2 Application of Ito’s Lemma to a Stock Price Process


8.1.3 The lognormal Distribution
It follows from this assumption that
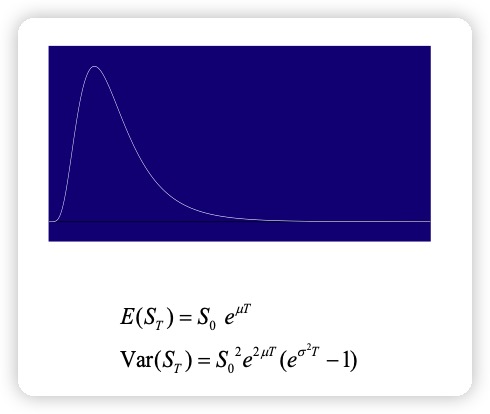
8.2 Derivation of The Black-Scholes-Merton Differential Equation
8.2.1 The Black-Scholes/Merton Model-Hedging Approach











8.2.2 Properties of Black-Scholes/Merton Formula


8.3 Implied Volatility
The implied volatility of an option is the volatility for which the Black-Scholes price equals the market price
第九章:股票指数期权和货币期权 Options On Stock Indices, Currencies, and Futures
9.1 Options on stock providing dividend
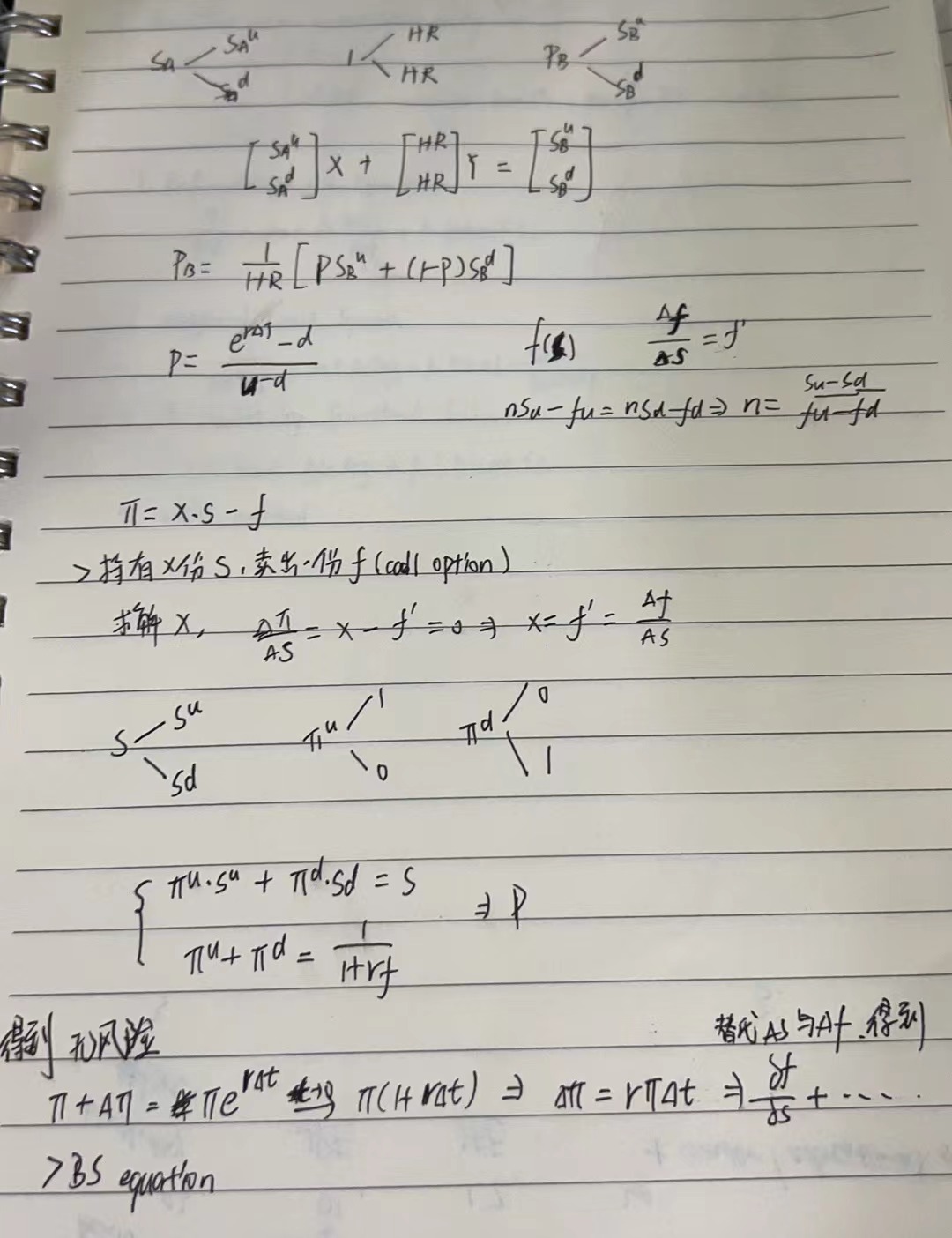
9.1.1 European Options on Stocks Providing a Dividend Yield
- The stock starts at price $S_0$ and provides a dividend yield = q
- The stock starts at prices $S_0e^{-qT}$ and provides no income
9.1.2 Lower Bounds For Option Prices
- $c \geq max(S_0 - Xe^{-rT}, 0)$
- $c \geq max(S_0e^{-qT} - Xe^{-rT}, 0)$
Lower Bound for calls:
$$c \geq S_0 e^{-qT} - Xe^{-rT}$$
- $p \geq max(Xe^{-rT} - S_0 , 0)$
- $p \geq max(Xe^{-rT} - S_0e^{-qT} , 0)$
Lower Bound for puts:
$$p \geq Xe^{-rT} - S_0 e^{-qT} $$
Put Call Parity
$$c + Xe^{-rT} = p + S_0e^{-qT}$$
American options Put Call Parity
$$S_0e^{-qT} - X \leq C - P \leq S_0 - Xe^{-rT}$$


9.2 Options on stock indices

9.3 Currency Options
9.4 Futures Option
9.4.1 Put-Call Parity for Futures Options
$$c + Ke^{-rT} = p + F_0e^{-rT}$$
$$F_0e^{-rT} - X \leq C - P \leq F_0 - X e^{-rT}$$


Value of the portfolio at time T is
$$F_0u\Delta - F_0\Delta - f_u = -f$$
and we obtain $f = -(F_0u\Delta - F_0\Delta - f_u)e^{-rT}$
Generalization
substituting the $\Delta$ we obtain
$$f = [pf_u + (1-p)f_d]e^{-rT}$$
$p = \frac{1-d}{u-d}$
第十章:希腊字母 Greek Letters
10.1 Common Strategies for Risk
10.1.1 Stop-Loss Strategy 止损策略
低抛高买
10.2 Delta Hedging
Delta ($\Delta$) (德尔塔对冲)is the rate of change of the option price with respect to the underlying asset.

10.2.1 Example
An investor has sold 20 call option contracts( 2,000 options ) on a certain stock. The option price is $10, the stock price is $100, and the option’s delta is 0.6. The investor wishes to hedge the position.
The strategy
The investor immediately buys 0.62000=1200 shares. It means that over the next short period of time, the call price will tend to change by 60% of the stock price and the loss (gain) on the call will be offset by the gain (loss) on the stock. As time passes, delta will change and the position in the stock will have to be adjusted. For example, if after three days the delta increases to 0.65, a further 0.052000=100 shares will have to be bought.
10.2.2 Dynamic Hedging
$$\Pi = -f + nS$$
$$\frac{\delta \Pi}{\delta S} = -\frac{\delta f}{\delta S} + n = 0$$
$$n = \frac{\delta f}{\delta S}$$
For a European call option on a non-dividend-paying stock
$$\Delta = N(d_1)$$For a European put option on a non-dividend-paying stock
$$\Delta = N(d_1) - 1$$The delta of a European call on a stock paying dividends at rate q
$$ \Delta = \frac{\delta f}{\delta S} = N(d_1)e^{-qT}$$The delta of a European put on a stock paying dividends at rate q
$$ \Delta = \frac{\delta f}{\delta S} = [N(d_1)-1]e^{-qT}$$
10.3 Theta, Gamma, Vega and Rho
10.3.1 Theta
Theta ($\Theta$ ) of a derivative (or portfolio of derivatives $\Pi$ ) is the rate of change of the value with respect to the passage of time, it is usually negative
$$\Theta = \frac{\delta f}{\delta t}$$
or
$$\Theta = \frac{\delta \pi}{\delta t}$$
10.3.2 Gamma
Gamma ($\Gamma$ ) is the rate of change of delta ($\Delta$) with respect to the price of the underlying asset
$$\Gamma = \frac{\delta^2 \Pi}{\delta S^2}$$
Gamma Addresses Delta Hedging Errors Caused By Curvature
10.3.2.1 Taylor Series Expansions and Hedge Parameters

10.3.2.2 Relationship Among Delta, Gamma, and Theta

10.3.3 Vega
Vega is the rate of change of the value of a derivatives portfolio with respect to volatility
$$V = \frac{\delta \Pi}{\delta \sigma}$$
Cause $Latex$ not support Vega using V substituting for Vega
10.3.4 [Example] Managing Delta, Gamma, & Vega

10.3.5 Rho
Rho is the rate of change of the value of a derivative with respect to the interest rate
$$\rho = \frac{\delta \Pi}{\delta r}$$
第十一章:Value-at-Risk(VaR) & Trading Strategies of Option
10.1 VaR
10.1.1 Types of VaR
VaR: 在正常市场条件下和一定的置信水平上,测算出给定时间内预期发生最坏情况的损失



10.1.2 Example S.D. of Portfolio


10.2 Trading Strategies Involving Options
10.2.1 Spread ( Two or more options of the same type)
10.2.1.1 Bull Spread Using Calls

10.2.1.2 Bull Spread Using Puts

10.2.1.3 Bear Spread Using Calls

10.2.1.4 Bear Spread Using Puts

10.2.1.5 Butterfly Spread Using Calls

10.2.1.6 Butterfly Spread Using Puts

10.2.1.7 Calendar Spread Using Calls

10.2.1.8 Calendar Spread Using Puts

10.2.2 Combination ( Mixture of calls & puts )
10.2.2.1 A Straddle(跨式) Combination
A straddle is appropriate when an investor is expecting a large move in a stock price but does not know in which direction the move will be

10.2.2.2 Strip
A strip consists of a long position in one call and two puts with the same strike price and expiration date

10.2.2.3 A Strangle (勒式)Combination
A strangle is a similar strategy to a straddle. The investor is betting that there will be a large price move, but is uncertain whether it will be an increase or a decrease




